Aproximando Ômega

Michael Winter

Gregory Chaitin me disse uma vez que apresentações em powerpoint tendem, com frequência, a se tornarem desinteressantes: ideias novas são mandadas embora – proibidas de se desenvolverem – em prol de pensamentos já conhecidos. Minha primeira introdução ao trabalho de Greg foi o vídeo de uma palestra sua sobre a Teoria da Informação Algorítmica (TIA). De forma coerente, ele se colocava em frente a um quadro negro, sem mostrar slides.

A maneira como Greg apresenta conceitos nunca está dissociada da potencialidade de explorar novas ideias. Mesmo quando explica entendimentos maduros sobre a TIA, desenvolvidos anos antes, ele por vezes inclina sua cabeça para cima, fecha os olhos, e parece abandonar momentaneamente a realidade. Podemos então especular que ele está formulando a próxima sentença, mas, se você tivesse a oportunidade de passar um longo tempo ao lado de Greg, veria que o retorno dele após esses breves afastamentos costuma ser acompanhado de uma revelação completamente nova. É uma forma de lembrar que, na maioria das vezes, novas ideias são fugidias, e, com frequência, efêmeras. Intuições criativas batem tão rápido que podem se perder se você não se retirar por um instante para explorá-las. Greg faz você desejar ter se permitido esses momentos tantas vezes quanto ele.

Quando assisti pela primeira vez aquela palestra, não entendi totalmente os conceitos da TIA, mas as ideias me disseram muito, e, algumas relações básicas com a música eram claras. Talvez, de forma mais ampla, a TIA fosse como uma prova de intuição. Portanto, se a matemática, o mais sagrado dos domínios, tinha axiomas que eram extremamente complexos, e, se a criatividade é, quem sabe, o segredo da nossa intuição, então aquilo que intuímos poderia ser, de fato, inovador.

Por um bom tempo, fui fascinado por filosofias digitais. Minha música costuma explorar processos simples na sua extensão lógica. Até onde vejo, vivemos em uma espécie de sopa de informação. Tudo é algoritmo, incluindo a música. Mas quando descobri o trabalho de Greg, ainda me equivocava, pois pensava que uma pessoa só poderia explorar ideias se evitasse a intuição, que eu considerava o panteão de um velho jardim coberto por ideias antigas com fachadas falsas de novidade. Não poderia estar mais enganado e, agora, com uma apreciação mais ampla da minha intuição e uma confiança maior em relação a como eu entendo o mundo empiricamente, gosto de pensar que, por causa disso, sou um músico muito melhor. Essa é uma lição que devo tanto a Greg, um matemático, quanto a outros músicos. Naquela época, tinha algum entendimento da incompletude de Gödel¹, mas as ramificações, para um músico, são muito mais evidentes nas provas de Chaitin, expressas pela linguagem de computadores e algoritmos, pois nelas certos conceitos normalmente levados em conta por músicos, tais como estrutura e aleatoriedade, são bem definidos. Não há dúvida de que muitos músicos se interessam, já faz tempo, pelo trabalho de Greg. Logo após minha introdução à TIA, descobri que muitos dos meus mentores e colegas mais próximos conheciam sua produção, incluindo Curtis Roads, Jim Tenney, Larry Polansky e Michael Pisaro. Larry, inclusive, havia convidado Greg para a Mills College, nos anos 1980 – mais tarde descobri uma pilha de papéis que Greg, depois de conhecer Larry, tinha enviado a Jim.

Quando visitei Nova York novamente, eu e Greg conseguimos nos encontrar em sua casa, em Westchester, onde ele vive parte do ano com sua mulher, Virginia (que é, também, uma importante epistemóloga). Desde então, nos tornamos amigos próximos e, gosto de pensar, colaboradores. Embora não diga que o meu trabalho tenha seguido os campos da TIA e da metabiologia, devo muito da minha música à relação que tenho com Greg e Virginia. Estou me referindo, em particular, aos trabalhos que diretamente estabelecem ou envolvem ideias de Greg, como Approximating Omega (uma peça que coloca um texto de Greg, destacando um de seus ‘brinquedos’² com a linguagem de programação LISP, e então sonoriza o programa que faz uma aproximação do número Ômega); for Gregory Chaitin (que sonoriza os primeiros 64 bits de um Ômega que Cristian Calude calculou); e quieting rooms (um modelo evolutivo simples, inspirado pela metabiologia, no qual o algoritmo tenta colocar dois sinais fora de fase). Recentemente visitei Greg e Virginia no Rio de Janeiro, onde encontrei Pedro Urano, aluno de Greg, que me convidou a escrever uma introdução à publicação de Approximating Omega incluída nesta publicação. Espero ressaltar aqui as conexões mais teóricas entre a TIA, a metabiologia e a música, concluindo com uma breve descrição de como a abordagem de Greg revela que a matemática é uma forma de arte.

Certamente meu entendimento de uma identificação com o trabalho de Greg foi antecedido pelo trabalho de Jim Tenney e Larry Polansky. Em particular, a tese “Meta+Hodos”, de Jim, tem uma colocação que sempre encorajou minha investigação contínua de formas.

“…(a estrutura) normalmente se refere mais a um aspecto interno do som –‘conexões’ ou inter-relações entre componentes cujas inter-relações não são necessariamente aparentes ‘na superfície’ da forma – por exemplo, em seu formato.”
Jim Tenney, em “Meta + Hodos”

Aqui, Jim claramente diz que a forma [form] compreende formato [shape] e estrutura. Vale mencionar que ao longo de “Meta+Hodos”, de modo sutil porém profundo, Jim incorpora conceitos da clássica Teoria da Informação de Shannon. Isso é facilmente percebido, dada a ênfase na psicologia Gestalt que se torna aparente no tratado seguinte, “META Meta+Hodos”, no qual Jim aplica diretamente as equações fundamentais da Teoria da Informação à análise da formação da Gestalt.

Mais tarde, Larry escreveria seu artigo seminal “Morphological Metrics”. Como sugere o título, Larry oferece um método para mensurar distâncias no espaço morfológico, onde uma morfologia é análoga àquilo que Jim chama de formato [shape]. Entretanto, eu argumentaria que algumas das métricas morfológicas de Larry podem ser melhor descritas como métricas estruturais (aquelas que envolvem a comparação de todos os elementos de paridade em uma morfologia, como opostos a simples elementos adjacentes).

Na época, eu explorava problemas musicais que a meu ver poderiam ser colocados como questões na Teoria dos Grafos. Isso me levou a um caminho particular pelo qual essa teoria poderia ser aplicada para a análise de música e que se tornou o ponto de partida da pesquisa para a minha tese “Structural Metrics”. Conforme o título, essa tese (contrária a de Larry) diz respeito àquele outro aspecto da forma. Por razões que, espero, se tornem evidentes mais tarde, o título mudou para “Structural Metrics: An Epistemology”.

A Teoria dos Grafos proporciona uma maneira interessante de representar e comparar estruturas musicais: vértices representam elementos musicais, e ângulos são induzidos entre elementos de paridade que satisfaçam algum tipo de relação a qual chamo de restrição morfológica local. Depois, se um grafo puder representar uma estrutura (fora do tempo), então um caminho no grafo poderia representar formato [shape] (no tempo), explicando portanto uma conexão intrínseca entre formato e estrutura.

Ainda acredito na viabilidade e na usabilidade de tal abordagem da Teoria dos Grafos, mas o meu foco mudou totalmente quando aprendi a respeito da TIA, pois claramente a codificação mais representativa de um objeto é o menor programa que irá computá-lo, o chamado programa elegante (cuja compressão é máxima). A estrutura é codificada no próprio programa, enquanto a morfologia é a saída [output].

 “Você tem uma lei da natureza, caso haja compressão e se os dados experimentais forem comprimidos em um programa de computador que possua um número menor de bits do que há nos dados que ele explica. Quanto maior o grau de compressão, melhor é a lei e mais compreensíveis são os dados. Mas se os dados experimentais não podem ser comprimidos…, se o menor programa para calculá-los é tão grande quanto eles, então os dados não possuem lei, são desestruturados…”
Gregory Chaitin, em “Meta Math!”

A TIA proporciona uma estrutura métrica objetiva: se o número mínimo de bits necessários para computar dois objetos juntos é significativamente menor do que a soma do número mínimo de bits necessários para computar cada objeto individualmente, então eles compartilham informações e são, portanto, próximos no espaço estrutural. Mas essa métrica requer que se conheça os programas elegantes de ambos objetos. Como Chaitin mostra na TIA, é impossível ter certeza de que se encontrou o programa elegante de uma determinada saída [output]. E é aqui que o Problema da Parada³ e o Paradoxo de Chaitin permeiam inclusive a música. À luz de tudo isso, minha tese se tornou uma sondagem epistemológica que, em comparação ao modelo objetivo de informações mútuas na TIA, apresenta o nível de empirismo em outras abordagens, como na Teoria dos Grafos. Quando concluí a tese, comecei de fato a entender de forma mais reflexiva o pressentimento inicial de quando assisti a palestra de Greg pela primeira vez: o trabalho dele é como uma prova de intuição. E de fato, o que Greg promove na matemática, uma abordagem mais empírica, vem sendo feito há muito pelos músicos.

Sou fundamentalmente um compositor e apenas um teórico amador da música. Com certeza não sou um matemático. No máximo, posso dizer que sou um músico seduzido pela matemática e pela ciência da computação. Ainda assim, meu entendimento de matemática – particularmente do trabalho de Greg – diz muito a respeito de como faço música e, mais ainda, de como vejo o mundo. No entanto, explorar os limites do conhecimento como um epistemólogo não é viável para um músico. Ao final do dia, um músico faz algo finito, efêmero e limitado pela praticidade. Ou seja, os limites epistemológicos estão muito além dos limites práticos habituais.

No meu trabalho, busquei reconciliar essa diferença fundamental. Approximating Omega talvez seja a ilustração que melhor se relaciona a essa reconciliação. Atualmente, computar o número de bits de um número Ômega é impossível. Entretanto, na minha peça de 2009, for Gregory Chaitin, eu sonorizo os primeiros 64 bits de um Ômega calculado por Cristian Calude. Em 2010, tive a ideia de sonorizar o programa de computador que realiza a aproximação de Ômega. Embora um número Ômega seja infinito, extremamente complexo e incomputável, os programas de Greg que se aproximam de Ômega são finitos, elegantes, estruturados e orientados pela gramática e sintaxe da linguagem: sub-rotinas são delimitadas e agrupadas por parêntesis; variáveis e funções se repetem etc. Escolhi particularmente a linguagem de programação LISP do livro de Greg “The Limits of Mathematics”, publicado em 1994, pois ela me permitia mapear facilmente cada caractere em relação a um som.

O mapeamento é simples: uma campainha aberta quando se abre parêntesis e uma fechada para quando se fecha parêntesis; um único som percussivo para todos os outros caracteres; e um único tom contínuo ao longo de qualquer configuração de delimitadores balanceados. Essa sonorização é a segunda parte da peça. A primeira metade é a apresentação de uma adaptação do texto do livro que explica as funções de um ‘programa-brinquedo’⁴ em linguagem LISP, o qual ressalta o mapeamento dos caracteres em relação ao som correspondente que é usado na segunda metade. O texto é lido por uma voz de fala normal, com pausas entre os parágrafos. Enquanto é lido o texto, o orador é acompanhado por uma delicada textura contínua ativada por outras pessoas do conjunto.

Em Approximating Omega, como no trabalho de Greg, somente o essencial é especificado. Não há sistemas. Aquilo que não é necessário para expressar uma ideia e reter os isomorfismos necessários entre várias performances – ou seja, a identidade do trabalho – é deixado em aberto. Condizentes com as ideias da TIA, as instruções buscam descrever minimamente como realizar uma peça. Aos meus ouvidos (e também aos de Greg, segundo ele me disse após ouvir a gravação de uma peça), a própria estrutura do programa se torna claramente audível quando a peça é realizada.

Essa é a reconciliação: enquanto a peça não coloca novas revelações sobre os limites epistemológicos nem se aproxima do número Ômega (já que são os caracteres do programa que são sonorizados em oposição a qualquer execução do programa), tudo relacionado à peça diz respeito à TIA, e tenho esperança que isso seja uma contribuição ao discurso sobre essa teoria.

Atualmente, Greg está trabalhando em ‘modelos de brinquedo’⁵ da evolução darwiniana, em um campo que ele chama de metabiologia. Isso é mais um exemplo da sua vivacidade: o início simultâneo de dois importantes domínios da matemática (a metabiologia acima da TIA), coerente com a sua personalidade de nunca estagnar e de continuamente explorar ideias radicais. E de fato, Greg é um radical. Seus deuses são ideias inovadoras, a beleza e o amor. Ele é rápido para indicar em que ponto a sociedade errou e para salientar que, se todos concordam com uma ideia desde o início, é sinal de que ela não é nova de forma alguma.

E ele está certo. Novas ideias radicais normalmente são desprezadas para não perturbar o status quo. Muitos matemáticos ainda ignoram as consequências da TIA (mesmo depois de Gödel, Turing, Kolmogoroff e Salomonoff) em prol de abordagens mais tradicionais. Suspeito que a aceitação da metabiologia (ou do que for que Greg tenha futuramente na manga) também levará tempo. Ao passo que o caráter inovador de uma ideia é finito – em algum momento ela é encerrada, ao ser aceita, estendida, evoluída e subsumida em um cânon –, imagino que, quanto mais radical/nova a ideia, mais tempo é necessário até sua aceitação geral. Interessante que esse conceito se reflete no tempo evolutivo da metabiologia (medido pelo número de mutações experimentadas entre evoluções sucessivas). Portanto, a metabiologia é um modelo de como as ideias evoluem e da evolução darwiniana. Vejo-me com frequência fazendo as seguintes analogias entre a metabiologia e a vida real: um organismo é uma ideia em evolução; uma evolução é um ato criativo; os algoritmos da mutação são, essencialmente, pessoas que podem ou não ser capazes de, mais tarde, desenvolver uma ideia; e a quantidade de tempo entre evoluções sucessivas é análoga à quantidade de tempo anterior à aceitação de uma ideia (pelo menos, até o ponto que alguém pode desenvolvê-la). Analogias à parte, ao combinar uma medida bem definida de tempo evolutivo com a ideia de mutações algorítmicas, Chaitin mostra que a evolução é contínua (ou então, visto de outra forma: o que é novo sempre se tornará velho) a um nível mais lento do que o de um projeto inteligente e mais rápido do que uma pesquisa exaustiva. Ele mostra isso da forma mais simples possível. Os modelos de brinquedo da metabiologia não possuem população e, portanto, sexo – tratam-se de apenas um único organismo em desenvolvimento.

Como músico, acho a falta de população e de sexo difícil de digerir (muito embora eu entenda, como discutirei mais tarde, o raciocínio de Greg). A música diz respeito a experiências compartilhadas e requer observadores. Embora minhas analogias acima reconciliem isso em certa medida, ao considerar os algoritmos de mutação como uma população, se eu tivesse maior destreza matemática, exploraria um modelo similar, com muitos organismos rodando em paralelo, em uma orgia constante de ideias compartilhadas (troca de informações). Nesse sentido, a música se parece muito ao sexo: um ato de partilha de informações. Muitas vezes tenho experiências musicais que me inspiram a tentar algo novo. Estou constantemente sendo estimulado [input] e transformo uma variedade de influências e experiências em novas músicas [output]. Elegância e criatividade são bem definidas, respectivamente, na TIA e na metabiologia. Mas sem população não há subjetividade e logo não há beleza (se você, como eu, também considera a beleza algo subjetivo). Independentemente disso, entendo porque o trabalho de Greg é tão focado e por que ele usa apenas o mais essencial para um teste, da mesma forma que eu faço ao criar uma peça musical. Seu trabalho nos lembra, de modo recorrente, que ideias elegantes podem revelar magnitudes de verdade as quais não veríamos se uma ideia fosse obscurecida pelo excesso de informação e explorada sem objetivo.

Greg costuma dizer que, se Deus existe, Ele deve ser um matemático. Entendo a colocação como uma reflexão a respeito da sua própria visão da natureza, pela qual o maior projeto de todos, o nosso universo, é belo em sua estrutura e devido às leis elegantes que o governam. Claro, minha resposta é: se Deus existe, ele deve ser um matemático com cabeça de músico (ou um músico com cabeça de matemático). Digo isso como uma forma de tornar explícito exatamente o que a abordagem de Greg nos mostra: a matemática, tanto quanto a música, é uma forma de arte. Com cada teste sucessivo em seu corpus, torna-se claro que valores estéticos matemáticos, tais como elegância e beleza, são tão importantes quanto o seu rigor. Aquilo que está sendo provado talvez seja menos importante do que a forma como é provado. Como na música, trata-se de compartilhar e evoluir.

Buenos Aires, julho 2014.

[1] http://pt.wikipedia.org/wiki/Teoremas_da_incompletude_de_G%C3%B6del
[2] ver nota 5
[3] http://pt.wikipedia.org/wiki/Problema_da_parada
[4] ver nota 5
[5] Em matemática, um modelo de brinquedo (ou toy model) é um modelo deliberadamente simplificado, em geral, pela redução do número de dimensões e/ou de campos/variáveis.

Aproximando Ômega

Nota (para ser usado como documento de apoio para performances, proporcionando recursos relacionados a essa peça):

Em artigo de 1975 intitulado “A theory of program size formally identical to information theory”, Gregory Chaitin define formalmente o número Ômega como a probabilidade de que um programa de computador, com bits gerados pelo lançar de uma moeda não viciada, interrompa uma máquina de Turing autodelimitada. O número Ômega é complexo em seu máximo e incomputável, porque nenhum algoritmo pode determinar se um programa de computador arbitrário será interrompido. O caráter indecidível do que hoje se conhece como “Problema da Parada” foi originalmente apresentado em 1936 por Alan Turing, no artigo “On computable numbers, with an application to the Entscheidungsproblem”, como corolário de uma prova computacional teórica do Teorema da Incompletude, de Kurt Gödel, apresentado primeiramente por Gödel em seu artigo “On formally undecidable propositions of Principia Mathematica and related systems I”, de 1931.

Embora o número Ômega seja incomputável, Chaitin desenvolveu um programa que se aproxima de Ômega com precisão crescente ao longo de períodos cada vez mais longos. O programa foi escrito em uma versão da linguagem LISP, que Chaitin estendeu e alterou a partir do protocolo criado inicialmente em 1958 por John McCarthy, com uma explicação publicada em seu artigo de 1960 “Recursive functions of symbolic expressions and their computation by machine”.

A primeira seção [opcional] dessa peça consiste em um orador que lê uma explicação do dialeto de LISP criado por Chaitin. Esse texto é uma adaptação do livro “The Limits of Mathematics”, publicado por Chaitin em 1994. Essa versão do LISP foi estendida pelo autor em 2001, no livro “Exploring Randomness”. A decisão de usar a versão mais antiga do LISP e de fazer mudanças no texto de “The Limits of Mathematics” tem propósito artístico e conta com a permissão do autor.

A segunda seção realiza o programa símbolo a símbolo, que se aproxima do número Ômega. Sons distintos (curtos, principalmente) representam cada símbolo, e as entradas e saídas de vários sons contínuos demarcam as expressões no programa. Portanto, o aninhamento de sub-rotinas no programa determina completamente a forma da música.

Los Angeles, 2010.

Instruções da performance:

Dinâmica e organização:
Todos os instrumentos devem soar em uma dinâmica uniforme, cada som sendo escutado claramente e sem estar alto. As fontes sonoras devem ser distribuídas pelo espaço da performance. A execução deve se ocupar principalmente do fenômeno sonoro em si.

Instrumentalização:
A parte 0 compreende uma bateria de 26 sons diferentes indicados por números. 0 e 1 indicam o tom (tom – ré; qualquer oitava fixa) de um instrumento de percussão com declínio natural longo. 0 é uma indicação para deixar ressoar.

1 indica um tom pontuado (rapidamente interrompido). Sons 0 e 1 ocorrem com mais frequência. Quando for possível, distribua essas ocorrências para o grupo de um instrumento específico (como 17 acordes de mesmo tom distribuídos pelo espaço da performance), de tal maneira que: quando vários 0s ocorram em sucessão, cada som tenha origem em uma fonte distinta; quando um 0 seja seguido rapidamente por um 1, a mesma fonte produza ambos os sons (ou seja, o tom que inicialmente se permite ressoar é interrompido pelo som pontuado que segue).

Cada número-som restante na parte 0 indica um som distinto, não-tom, que é curto e/ou possui uma decaída natural longa. Distribua o quanto puder as fontes desses sons pelo espaço da performance. Cada parte de 1 a 17 deve ser distinguida unicamente pelo timbre e/ou tom. Um performer pode jogar várias partes com paradas duplas, instrumentos múltiplos, sons polifônicos sintetizados ou gravados etc. Atribua a cada parte tocada por um instrumento de tons determinados um tom distinto, derivado de uma das primeiras 17 partes principais da série harmônica de ré. Os nomes das notas com desvios centesimais (um centésimo de um semitom da escala temperada) são oferecidos acima da tabela na Seção 2. Os performers podem soar um tom (pitch-class) respectivo a uma parte em qualquer oitava e podem mudar oitavas para cada novo tom.

Seção 1 (opcional):
O texto é lido por uma voz ritmada com silêncios de durações variadas entre cada parágrafo (delimitado por quebras de linhas duplas). Subgrupos variados do conjunto acompanham cada parágrafo, iniciando e terminando precisamente com o orador. Em cada parágrafo, o som que acompanha deve soar como um única configuração. Os sons devem soar de forma contínua, embora os instrumentos de percussão possam escolher soar uma série de pontuados ataques rapidamente repetidos em tempos individuais. Instrumentos específicos podem entrar e sair livremente, desde que uma continuidade geral seja mantida. Símbolos dentro de colchetes não são pronunciados. Em vez disso, soa um tom correspondente ao número-som da Parte 0 (informado na coluna da esquerda). Preceda e suceda esse som com silêncio. Interpreta-se que o parágrafo começa na linha seguinte. Uma palavra entre aspas coincide com o som de um tom correspondente ao número-som da Parte 0 (também informado na coluna da esquerda). Palavras sublinhadas não são faladas nem acompanhadas. Os performers da Parte 0 devem tocar quando há indicações de colchetes e aspas no texto, mas também podem contribuir com o som mais contínuo que acompanha cada parágrafo.

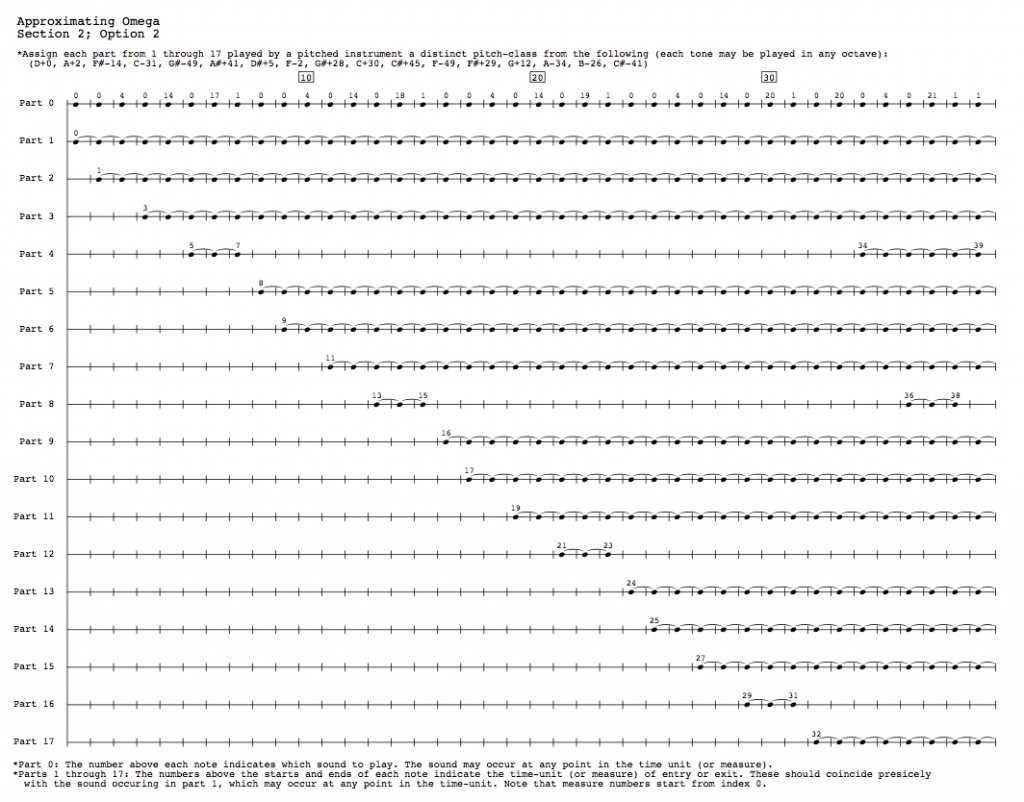
Seção 2:
A Parte 0 é pontuada como uma lista de pares. O primeiro número é uma unidade-tempo na qual ocorre um som indicado pelo segundo número. Duas colunas oferecem opções para as 17 partes restantes (organizadas em colunas). A coluna contém uma lista de pares de unidade-tempo para os momentos iniciais e finais de cada tom. Os tons devem entrar e existir precisamente com o som da Parte 0 acontecendo na mesma unidade-tempo. O conjunto pode escalar uniformemente as unidades-tempo por qualquer quantidade. Repare que, na Opção 1, quanto maior o número da parte, menores se tornam as durações gerais dos tons. A Opção 2 sacrifica isso em troca de partes que são mais uniformemente ativas. Partituras mais tradicionalmente pontuadas também são oferecidas para ambas opções. Um apêndice dá a lista de pares de tempo, sem atribuição de partes. O conjunto pode explorar a distribuição desses tons de outras formas, mas ela sempre terá pelo menos 17 partes.

Seção 1:
Parte 0:                                  Orador com acompanhamento

O número Ômega é definido formalmente como a probabilidade de que um programa de computador, com bits gerados pelo lançar de uma moeda não viciada, interrompa um computador genérico autodelimitado. Como nenhum algoritmo pode determinar a interrupção de um programa de computador arbitrário, o número Ômega é complexo de forma máxima e incomputável. Entretanto, existe uma computação que se aproxima de Ômega com precisão crescente ao longo de períodos cada vez mais longos. Nós destacamos esse método em uma versão alterada e estendida da linguagem de programação LISP.

A LISP assemelha-se mais a matérias fundamentais, como a teoria dos conjuntos e a lógica, do que a uma linguagem tradicional de programação. O formalismo da LISP consiste em várias funções primitivas e em um grupo de regras para a definição de funções mais complexas a partir das funções primitivas iniciais. As funções da LISP são tecnicamente conhecidas como funções recursivas parciais. Definições de dados e funções da LISP consistem em expressões-S. “S” refere-se a “simbólico”.

Expressões-S são listas que consistem em delimitadores de início e fim, conectando zero ou mais elementos, os quais podem ser átomos ou sublistas. Formalmente, a classe de expressões-S é a união da classe de átomos e da classe de listas.

O conceito semântico fundamental da LISP diz respeito ao valor de uma expressão-S em um dado ambiente. Um ambiente consiste em uma lista associada na qual variáveis (átomos) e seus valores (expressões-S) se alternam. Se uma variável aparece várias vezes, somente seu primeiro valor é significativo. Se uma variável não aparece no ambiente, então ela é uma constante literal em que ela própria é o seu valor.

A LISP reserva os seguintes símbolos, entendidos com um nome, um número de argumentos (se aplicável) e uma explicação. Exceto os quatro primeiros, todos representam funções primitivas.

0
Símbolo: [(]
Nome: Delimitador-início
Explicação: Denota o começo de uma expressão-S.

1
Símbolo: [)]
Nome: Delimitador-fim
Explicação: Denota o fim de uma expressão-S.

2
Símbolo: [1]
Nome: Verdadeiro
Explicação: Denota o valor de verdade.

3
Símbolo: [0]
Nome: Falso
Explicação: Denota o valor de falso.

4
Símbolo: [’]
Nome: Aspas ou Literalmente
Argumentos: 1
Explicação: O resultado da aplicação dessa função é a expressão de argumento não avaliado.

5
Símbolo: [.]
Nome: Átomo
Argumentos: 1
Explicação: O resultado da aplicação dessa função a um argumento é verdadeiro ou falso dependendo se o argumento é ou não um átomo.

6
Símbolo: [=]
Nome: Igual
Argumentos: 2
Explicação: O resultado da aplicação dessa função é verdadeiro ou falso dependendo se os dois argumentos são ou não a mesma expressão-S.

7
Símbolo: [+]
Nome: Cabeça ou Primeiro
Argumentos: 1
Explicação: O resultado da aplicação dessa função a um átomo é o próprio átomo. O resultado da aplicação dessa função a uma lista não vazia é o primeiro elemento da lista.

8
Símbolo: [-]
Nome: Cauda ou Resto
Argumentos: 1
Explicação: O resultado da aplicação dessa função a um átomo é o próprio átomo. O resultado da aplicação dessa função a uma lista não vazia são os elementos restantes após a supressão do primeiro elemento. Portanto, a cauda de uma lista de elemento-(n + 1) é uma lista elemento-n.

9
Símbolo: [*]
Nome: Unir
Argumentos: 2
Explicação: Se o segundo argumento não é uma lista, então o resultado da aplicação dessa função é o primeiro argumento. Se o segundo argumento é uma lista de elemento-n, então o resultado da aplicação dessa função é a lista elemento-(n+ 1) cuja cabeça é o primeiro argumento e cuja cauda é o segundo argumento.

10
Símbolo: [,]
Nome: Apresentar
Argumentos: 1
Explicação: O resultado da aplicação dessa função é o seu argumento e é usado para apresentar resultados intermediários. Em outras palavras, essa é uma função de identidade. É a única função primitiva com um efeito colateral, o qual é apresentar o argumento.

11
Símbolo: [/]
Nome: Se-então-outro
Argumentos: 3
Explicação: Se o primeiro argumento não é falso, então o resultado é o segundo argumento. Se o primeiro argumento é falso, então o resultado é o terceiro argumento. O argumento que não é selecionado não é avaliado.

12   Símbolo: [!]
Nome: Avaliar
Argumentos: 1
Explicação: A expressão que é o valor do argumento é avaliada em um ambiente vazio. Essa é a única função primitiva que é uma parcial ao invés de uma função total.

13
Símbolo: [?]
Nome: Tentativa ou Avaliação de Profundidade Limitada
Argumentos: 2
Explicação: A expressão que é o valor do segundo argumento é avaliada em um ambiente vazio. O número de elementos do primeiro argumento dá um limite de tempo (ou seja, um número máximo de computações igual à duração da lista ou zero, se o primeiro argumento não é uma lista). De fato, o limite de tempo limita a profundidade da avaliação. Se a avaliação se completa dentro do limite de tempo, o valor devolvido é uma lista cujo único elemento é o valor da expressão que é o valor do segundo elemento. Se a avaliação não se completa dentro limite de tempo, o valor devolvido é o átomo para “Tentativa”.

14
Símbolo: [&]
Nome: Defina Função ou Lambda
Argumentos: 2
Explicação: Tratado essencialmente como uma função primitiva, esse átomo é usado para criar uma função definida na qual o primeiro argumento é uma lista de variáveis e o segundo argumento é o corpo da definição da função. Observe que todos os outros símbolos (não-reservados) podem ser usados como variáveis em uma função definida.

Nós estendemos a LISP para definir um computador genérico auto-delimitador. O programa do computador aparece em sua fita como uma representação binária de uma expressão LISP. Observe que o programa deve ser auto-delimitador, pois a expressão-S deve ter delimitadores equilibrados.

13
Redefinimos “Tentativa” com o acréscimo de um argumento capaz de colocar, incialmente, informações na fita do computador. Os três argumentos são conforme segue. O primeiro, a profundidade-limite, é uma alteração da definição original da LISP: se é um átomo não nulo, então não há limite de profundidade; se é a lista vazia, há limite de profundidade zero (ou seja, nenhuma chamada de função ou reavaliações); se é uma lista de elemento-n, há um limite de profundidade de n. O segundo argumento é conforme anteriormente: a expressão a ser avaliada na medida em que o limite de profundidade não é excedido. O novo terceiro argumento é uma lista de bits a ser usada como a fita do programa de computador.

13
O valor devolvido por “Tentativa” também mudou. Se a computação termina normalmente, o primeiro elemento do valor devolvido é uma lista com só um elemento, o qual é o resultado da computação. Se a avalição do segundo
12
argumento é abortada, o primeiro elemento do valor devolvido é o átomo para “Avalie”, após uma tentativa de
13
ler um bit não existente da fita ou do átomo para “Tentativa”, quando o número de computações excede o limite
10
de tempo. O resto do valor devolvido é uma pilha de todos os argumentos para a função primitiva “Apresentar” encontrada durante a avaliação do segundo argumento.

Reservamos mais dois símbolos para primitivas que poderiam ser programadas, mas que são embutidas para ajudar a definir convenientemente e a rodar de forma eficaz um computador genérico auto-delimitador.

15
Símbolo: [^]
Nome: Anexo
Argumentos: 2
Explicação: O resultado dessa função é a concatenação de seus dois argumentos em uma única lista.

16
Símbolo: [%]
Nome: Expressão-Ler
Explicação: Leia uma expressão LISP inteira da fita do computador. Essa função é a única forma de acessar a informação na fita do computador. Deve ser implementada de modo auto-delimitador, pois nenhum algoritmo pode procurar o fim da fita e então usar a duração da fita como dado na computação. Se um algoritmo tenta ler um bit que não está na fita, o algoritmo aborta. Ou seja, a função explode caso a fita se esgote, matando a computação.

Concluindo, a permissividade da nossa LISP é alcançada pois funções com argumentos extras são avaliadas, mas ignoradas, e listas vazias são abastecidas para argumentos que faltam. Não há expressões errôneas, somente expressões que nunca devolvem um valor, pois o intérprete entra em um ciclo infinito.

Aproximando Ômega:

Seção 2:
((‘(&(V)((‘(&(A)((‘(&(R)((‘(&(W)(W(‘(O)))))(‘(&(n)(*0(*.(R(Vn())n))))))))(‘(&(xy)(/(.x)(/(.y)()(*0(Rx(-y))))(^(R(-x)(y))(*(+x)()))))))))(‘(&(xyz)(/(.x)(/(.y)(/z(‘(1))())(A(‘(0))yz))(/(.y)(Ax(‘(0))z)(*(=(+x)(=(+y)z))(A(-x)(-y)(/(+x)(/(+y)1z)(/(+y)z0)))))))))))(‘(&(xy)(/(.x)(/(.(+(?n(‘(!(%)))y)))()(‘(1)))(A(V(-x)(*0y))(V(-x)(*1y))0)))))

Acima é o programa aproximando-se de Ômega, dado em sua representação ascii. Observe que o símbolo O representa uma lista de 1s com uma duração que determina quantos bits da expansão binária de Ômega são aproximados.

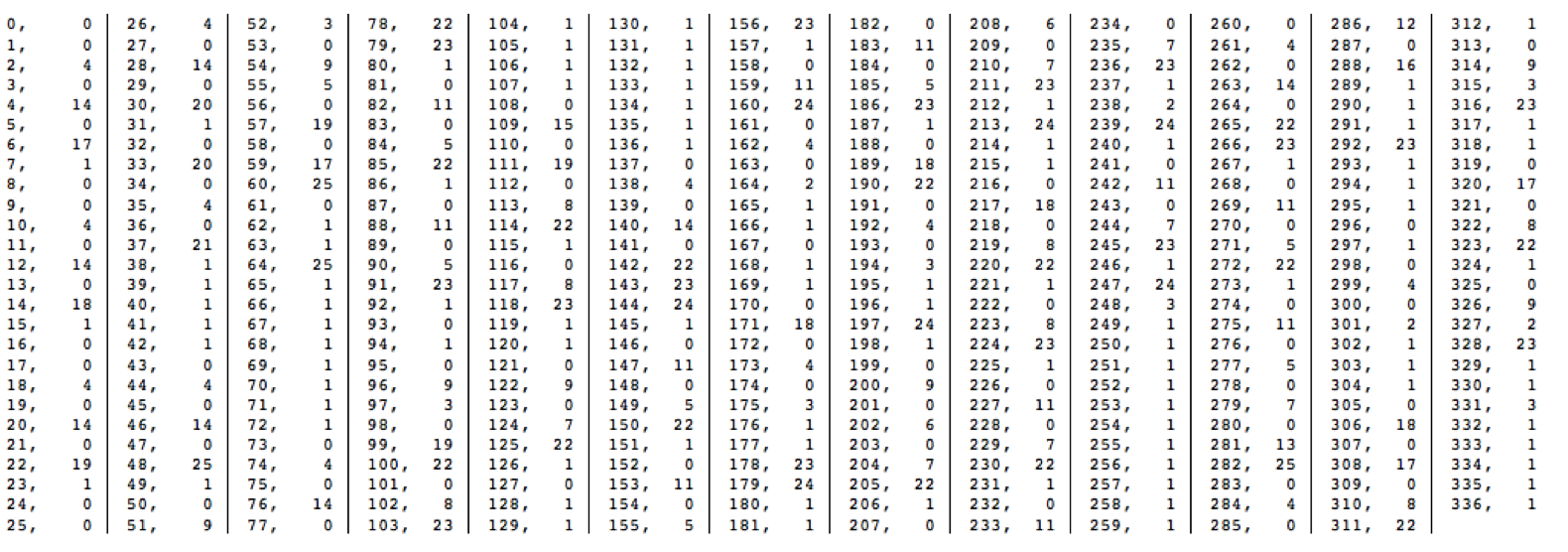
Parte 0 (unidade-tempo, som):

Atribua a cada parte tocada por um instrumento de tons determinados um tom distinto entre os seguintes:
(D+0, A+2, F#-14, C-31, G#-49, A#+41, D#+5, F-2, G#+28, C+30, C#+45, F-49, F#+29, G+12, A-34, B-26, C#-41)

Opção 1 (início unidade-tempo, unidade tempo-final):

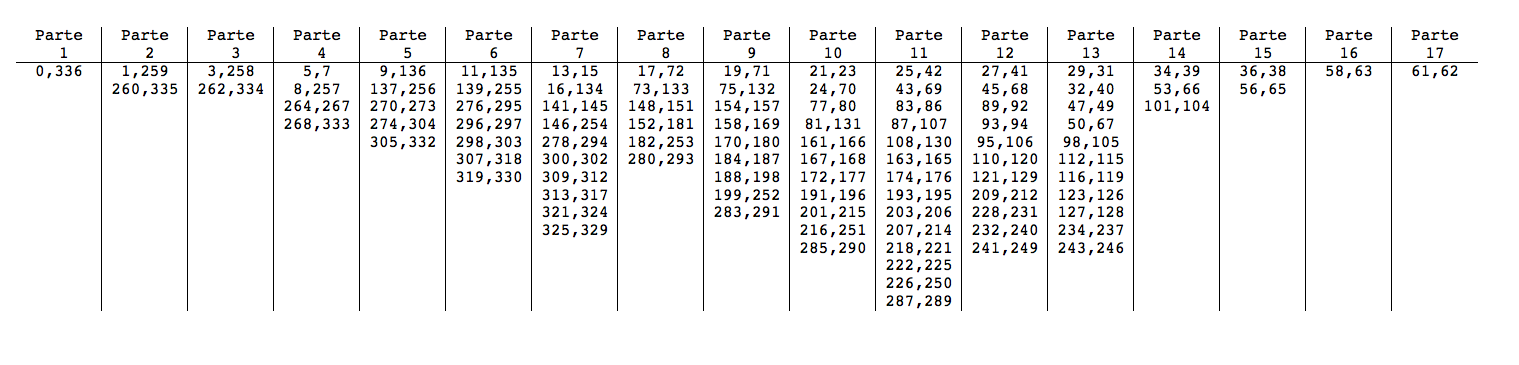Opção 2 (início unidade-tempo, unidade tempo-final):

Apêndice
Tons contínuos (início unidade-tempo, unidade tempo-final):
((0,336),(1,259),(3,258),(5,7),(8,257),(9,136),(11,135),(13,15),(16,134),(17,72),(19,71),(21,23),(24,70),(25,42),(27,41),(29,31),(32,40),(34,39),(36,38),(43,69),(45,68),(47,49),(50,67),(53,66),(56,65),(58,63),(61,62),(73,133),(75,132),(77,80),(81,131),(83,86),(87,107),(89,92),(93,94),(95,106),(98,105),(101,104),(108,130),(110,120),(112,115),(116,119),(121,129),(123,126),(127,128),(137,256),(139,255),(141,145),(146,254),(148,151),(152,181),(154,157),(158,169),(161,166),(163,165),(167,168),(170,180),(172,177),(174,176),(182,253),(184,187),(188,198),(191,196),(193,195),(199,252),(201,215),(203,206),(207,214),(209,212),(216,251),(218,221),(222,225),(226,250),(228,231),(232,240),(234,237),(241,249),(243,246),(260,335),(262,334),(264,267),(268,333),(270,273),(274,304),(276,295),(278,294),(280,293),(283,291),(285,290),(287,289),(296,297),(298,303),(300,302),(305,332),(307,318),(309,312),(313,317),(319,330),(321,324),(325,329));

 Tradução: Ricardo Romanoff

***

MICHAEL WINTER é compositor, teórico musical e designer de software. É co-fundador e diretor da organização artística sem fins lucrativos The Wulf, que realiza apresentações musicais gratuitas em Los Angeles, onde o artista vive e trabalha.
http://www.unboundedpress.org/

Baixe o arquivo de “Aproximating Ômega” em inglês, na versão pdf com formatação original do autor: Approximating_Omega.

Todos os direitos reservados.